Επιστήμη - Επιστημολογία
- Το θεώρημα της μη πληρότητας και φιλοσοφικές προεκτάσεις
- Η ελευθερία του απροσδιόριστου
- Σχετικότητα και προεκτάσεις
- Θεωρία της σχετικότητας: οι έννοιες
- Κβαντομηχανική: έννοιες και ερμηνευτικά ρεύματα
- Eρμηνείες της κβαντoμηχανικής: Ο Schrodinger και η γάτα του
- Προς μια θεωρία των πάντων
- Οικοσύνθεση στον Άρη
- Διαλεκτική βιολογία
- Οι αντιλήψεις του Schrodinger για το "Τι είναι η ζωή"
Θεωρία της σχετικότητας: οι έννοιες
3) Ο χωρόχρονος
Μέχρι τώρα εξετάσαμε μόνο ευθύγραμμες κινήσεις. Το Σ.Σ. μας ήταν μια σταθερή ράβδος που είχε αρχή και δεν είχε τέλος. Θα διατηρήσουμε αυτό τον περιορισμό και θα πάρουμε διάφορα σημεία πάνω στη ράβδο: Οι θέσεις τους μπορούν να καθοριστούν από την τετμημένη του σημείου κι αντίθετα, σε κάθε τετμημένη αντιστοιχεί το αντίστοιχο σημείο πάνω στη ράβδο.
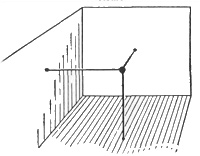
Αυτό εκφράζεται με την πρόταση: όλα τα σημεία πάνω στη ράβδο, αποτελούν ένα μονοδιάστατο συνεχές. Η αυθαίρετη μικρότητα των βημάτων που συνδέουν δυο απομακρυσμένα σημεία, είναι χαρακτηριστικό του συνεχούς. Ένα επίπεδο είναι ένα δισδιάστατο συνεχές ενώ ο χώρος είναι ένα τρισδιάστατο συνεχές.
Για να επιστρέψουμε στη φυσική, πρέπει να θεωρήσουμε την κίνηση υλικών σωματιδίων. Για να παρατηρήσουμε και να προβλέψουμε φυσικά φαινόμενα, πρέπει να λάβουμε υπ' όψη μας όχι μονάχα τη θέση, αλλά και τα χρόνο στον οποίο πραγματοποιούνται.
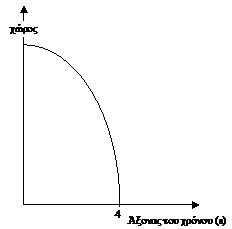
Ας πάρουμε το παράδειγμα της ελεύθερης πτώσης ενός σώματος. Η πτώση σ' ένα μονοδιάστατο χώρο, παριστάνεται εδώ από μια καμπύλη σ' ένα δισδιάστατο χωροχρονικό συνεχές. Σε κάθε σημείο του χωροχρονικού μας συνεχούς αντιστοιχεί ένα ζευγάρι αριθμών, από τους οποίους ο ένας δηλώνει την συντεταγμένη του χρόνου και ο άλλος τη συντεταγμένη του χώρου. Αντίστροφα: ένα ορισμένο σημείο στο χωροχρονικό μας επίπεδο, αντιστοιχεί σε κάθε ζευγάρι αριθμών πού χαρακτηρίζουν ένα γεγονός. Δυο γειτονικά σημεία αντιπροσωπεύουν δυο γεγονότα πού έγιναν σε θέσεις και σε χρόνους ελαφρά διαφορετικούς. (Με αυτά δεν ενώνουμε τον χώρο με τον χρόνο. Απλά χρησιμοποιούμε μια δυναμική παράσταση όπου οι θέσεις αλλάζουν με το χρόνο).
Μπορούμε ωστόσο την ίδια κίνηση να την παραστήσουμε με διαφορετικά τρόπο. Μπορούμε να κάνουμε μια στατικήπαράσταση, θεωρώντας την καμπύλη σ’ ένα δισδιάστατο χωροχρονικά συνεχές. Η κίνηση παριστάνεται τώρα σαν κάτι που είναι, που υπάρχει σε ένα δισδιάστατο χωροχρονικό συνεχές, και όχι σαν κάτι που μεταβάλλεται σ' ένα μονοδιάστατο χωρικό συνεχές.
Οι δυο αυτές παραστάσεις είναι αυστηρά ισοδύναμες και είναι ζήτημα σύμβασης να προτιμάμε τη μια από την άλλη.
Τίποτα απ' όσα ειπώθηκαν εδώ για τις δυο παραστάσεις της κίνησης, δεν έχει σχέση με τη θεωρία της σχετικότητας. Οι δυο παραστάσεις μπορούν να χρησιμοποιούνται ισοδύναμα, αν και η κλασική φυσική προτιμούσε κυρίως τη δυναμική παράσταση, περιγράφοντας την κίνηση σαν σειρά γεγονότων στο χώρο και όχι στο χωροχρόνο. Αλλά η θεωρία της σχετικότητας, άλλαξε αυτή τη σκοπιά. Είναι σαφώς υπέρ της στατικής εικόνας και βρήκε σε τούτη την παράσταση της κίνησης μια πιο αντικειμενική εικόνα της πραγματικότητας. Αλλά γιατί αυτές οι δυο παραστάσεις, που από την κλασική σκοπιά είναι ισοδύναμες, δεν είναι κι από την άποψη της θεωρίας της σχετικότητας;
Θα μπορέσουμε να απαντήσουμε, αν ξαναδούμε δυο Σ.Σ. με ομαλή σχετική κίνηση.
Σύμφωνα με την κλασική φυσική, παρατηρητές σε δυο Σ.Σ. με σχετική ομαλή κίνηση, θα αποδώσουν σε ένα καθορισμένο γεγονός διαφορετικές συντεταγμένες του χώρου, αλλά την ίδια χρονική συντεταγμένη. Στο παράδειγμα της ελεύθερης πτώσης, η σύμπτωση του σωματιδίου με το έδαφος χαρακτηρίζεται στο Σ.Σ. που εκλέξαμε από τη συντεταγμένη του χρόνου «4» και τη συντεταγμένη του χώρου «μηδέν». Σύμφωνα με την κλασική μηχανική, το χαλίκι θα φτάσει το έδαφος ύστερα από τέσσερα δευτερόλεπτα και για έναν παρατηρητή με ομαλή κίνηση ως προς το Σ.Σ. πού εκλέξαμε. Αυτός ο παρατηρητής θα αναφέρει ωστόσο την απόσταση στο Σ.Σ. του, και θα αποδώσει γενικά διαφορετικές χωρικές συντεταγμένες στα γεγονός της κρούσης. Για κάθε Σ.Σ., το δισδιάστατο συνεχές μπορεί να χωριστεί σε δυο μονοδιάστατα συνεχή: χρόνο και χώρο.
Σύμφωνα με τη θεωρία της σχετικότητας, όμως, ο χρόνος που το χαλίκι θα αγγίξει τη γη, δεν θα είναι ο ίδιος για όλους τους παρατηρητές. Η συντεταγμένη του χρόνου και η συντεταγμένη του χώρου θα είναι διαφορετικές σε δυο διαφορετικά Σ.Σ. και η μεταβολή στη συντεταγμένη του χρόνου θα είναι πολύ έντονη, αν η σχετική ταχύτητα πλησιάζει την ταχύτητα του φωτός. Το δισδιάστατο συνεχές δε μπορεί να χωριστεί σε δυο μονοδιάστατα, όπως στην κλασική φυσική. Δεν πρέπει να εξετάζουμε τα χώρο και το χρόνο χωριστά, όταν καθορίζουμε τις χωροχρονικές συντεταγμένες σε ένα άλλο Σ.Σ. Ο χωρισμός του δισδιάστατου συνεχούς σε δυο μονοδιάστατα, είναι αυθαίρετος και δεν έχει αντικειμενικό νόημα.
Είναι εύκολο να επεκτείνουμε όσα είπαμε, στην περίπτωση που η κίνηση γίνεται σε τρεις χωρικές διαστάσεις. Η χρονική στιγμή ενός γεγονότος είναι ο τέταρτος αριθμός. Σε κάθε γεγονός αντιστοιχούν τέσσερις ορισμένοι αριθμοί κι αντίστροφα ένα ορισμένο γεγονός, αντιστοιχεί σε τέσσερις αριθμούς. Έτσι κόσμος των γεγονότων, αποτελεί ένα τετραδιάστατο συνεχές. Η τελευταία πρόταση είναι αληθινή για την κλασική φυσική, όσο και για τη θεωρία της σχετικότητας. Η διαφορά παρουσιάζεται όταν μελετούμε δυο Σ.Σ. με σχετική κίνηση. Το δωμάτιο κινείται, και ο εσωτερικός και εξωτερικός παρατηρητής προσδιορίζουν τις χωροχρονικές συντεταγμένες των ίδιων γεγονότων. Ο κλασικός φυσικός χωρίζει πάλι το τετραδιάστατο συνεχές, σε τρισδιάστατο χωρικό συνεχές και το μονοδιάστατο χρονικό. Αλλά κατά τη θεωρία της σχετικότητας, τόσο ο χρόνος όσο κι ο χώρος μεταβάλλονται όταν περνά κανείς από ένα Σ.Σ. σε άλλο. Οι μετασχηματισμοί του Lorentz καθορίζουν τις ιδιότητες μετασχηματισμού του τετραδιάστατου κόσμου των γεγονότων.
Ο κόσμος των γεγονότων μπορεί να περιγραφεί δυναμικά με μια εικόνα που μεταβάλλεται με το χρόνο και που προβάλλεται στο φόντο του τρισδιάστατου χώρου. Αλλά μπορεί να περιγραφεί και με μια στατική εικόνα, στο φόντο του τετραδιάστατου χωροχρονικού συνεχούς. Από την άποψη της κλασικής φυσικής, οι δυο εικόνες, δυναμική και στατική, είναι ισοδύναμες. Από την άποψη της θεωρίας της σχετικότητας, ή στατική εικόνα είναι πιο βολική και πιο αντικειμενική.
Ακόμα και στη θεωρία της σχετικότητας μπορούμε, αν το προτιμάμε, να χρησιμοποιούμε τη δυναμική εικόνα. Αλλά πρέπει να θυμόμαστε πως ο χωρισμός αυτός σε χώρο και χρόνο δεν έχει αντικειμενικό νόημα, μια και ο χρόνος δεν είναι πια «απόλυτος». Ωστόσο, στα παρακάτω θα χρησιμοποιούμε πάντα τη «δυναμική» και όχι τη «στατική» γλώσσα.
Μετάβαση σε άλλη ενότητα του άρθρου: