Επιστήμη - Επιστημολογία
- Το θεώρημα της μη πληρότητας και φιλοσοφικές προεκτάσεις
- Η ελευθερία του απροσδιόριστου
- Σχετικότητα και προεκτάσεις
- Θεωρία της σχετικότητας: οι έννοιες
- Κβαντομηχανική: έννοιες και ερμηνευτικά ρεύματα
- Eρμηνείες της κβαντoμηχανικής: Ο Schrodinger και η γάτα του
- Προς μια θεωρία των πάντων
- Οικοσύνθεση στον Άρη
- Διαλεκτική βιολογία
- Οι αντιλήψεις του Schrodinger για το "Τι είναι η ζωή"
Θεωρία της σχετικότητας: οι έννοιες
5) Η νέα αντίληψη για τα «μη αδρανειακά» συστήματα
Ας φανταστούμε ένα μεγάλο ανελκυστήρα, στο τελευταίο πάτωμα ένας ουρανοξύστη. Το συρματόσκοινο που κρατάει τον ανελκυστήρα σπάει κι ο ανελκυστήρας αρχίζει να πέφτει ελεύθερα. Παρατηρητές μέσα στον ανελκυστήρα, κάνουν πειράματα στη διάρκεια της πτώσης σε ιδεώδεις συνθήκες. Ένας από τους παρατηρητές βγάζει από την τσέπη του ένα μαντήλι και ένα ρολόι και τα αφήνει ελεύθερα. Για τον εξωτερικά παρατηρητή, πού βλέπει μέσα από ένα παράθυρο του ανελκυστήρα, το ρολόι και το μαντήλι πέφτουν ακριβώς με τον ίδιο τρόπο, με την ίδια επιτάχυνση, (δεδομένης της ισότητας της αδρανούς και της βαρείας μάζας). Η ισότητα των δυο μαζών ήταν, συμπωματική από την άποψη της κλασικής μηχανικής και δεν έπαιζε ρόλο στη δομή της. Εδώ όμως η ισότητα αυτή, που αντικαθρεφτίζεται στη ίση επιτάχυνση πτώσης όλων των σωμάτων, είναι ουσιώδης και αποτελεί τη βάση όλης της συλλογιστικής.
Ας ξαναρθούμε στο μαντήλι και στο ρολόι πού πέφτουν: για τον εξωτερικό παρατηρητή και τα δυο πέφτουν με την ίδια επιτάχυνση. Αλλά το ίδιο συμβαίνει και για τον ανελκυστήρα και η απόσταση ανάμεσα στο πάτωμα και τα δυο σώματα, δε θα μεταβληθεί. Για τον εσωτερικό παρατηρητή, τα δύο σώματα μένουν ακριβώς εκεί πού ήταν όταν τα άφησε ελεύθερα. Ο εσωτερικός παρατηρητής μπορεί να αγνοεί το πεδίο βαρύτητας, γιατί η πηγή του βρίσκεται έξω από το Σ.Σ. του. Βρίσκει πως καμιά δύναμη δε δρα πάνω στα δυο σώματα στο εσωτερικό του ανελκυστήρα σαν να βρίσκονταν σε αδρανειακό σύστημα. Αν ο παρατηρητής σπρώξει ένα σώμα προς οποιαδήποτε κατεύθυνση, το σώμα θα κινείται ομαλά. Έτσι, οι νόμοι της κλασικής μηχανικής ισχύουν για τον εσωτερικό παρατηρητή. Όλα τα σώματα συμπεριφέρνονται σύμφωνα με την αρχή της αδράνειας. Το νέο Σ.Σ. μας, σταθερά δεμένο με τον ανελκυστήρα που πέφτει ελεύθερα, διαφέρει από το σύστημα αδράνειας μόνο από μια άποψη: Ο αδρανειακός χαρακτήρας του Σ.Σ. του ανελκυστήρα είναι περιορισμένος στο χώρο και στο χρόνο. Αργά ή γρήγορα το σώμα με την ομαλή κίνηση θα χτυπήσει σε μια πλευρά του ανελκυστήρα και η ομαλή του κίνηση θα καταστραφεί καθώς ο ανελκυστήρας θα συγκρουστεί με τη γη.
Ο τοπικός χαρακτήρας του Σ.Σ. έχει ουσιαστική σημασία. Αν ο φανταστικός ανελκυστήρας μας έφτανε από το βόρειο πόλο ως τον ισημερινό, κι αν αφήναμε να πέσει το μαντήλι πάνω από τον πόλο και το ρολόι πάνω από τον ισημερινό, τότε τα δυο σώματα δεν θα είχαν την ίδια επιτάχυνση για τον εξωτερικό παρατηρητή. Έτσι οι διαστάσεις του ανελκυστήρα πρέπει να είναι περιορισμένες, ώστε να μπορεί να θεωρηθεί ότι υφίσταται η ισότητα της επιτάχυνσης όλων των σωμάτων ως προς τον εξωτερικό παρατηρητή.
Με αυτό τον περιορισμό, το Σ.Σ. έχει το χαρακτήρα συστήματος αδράνειας για τον εσωτερικό παρατηρητή. Αν φανταστούμε ένα άλλο Σ.Σ., έναν άλλον ανελκυστήρα που κινείται ομαλά ως προς τον ανελκυστήρα που πέφτει ελεύθερα, τότε αυτά τα δυο Σ.Σ. θα είναι τοπικά συστήματα αδράνειας. Όλοι οι νόμοι είναι οι ίδιοι και στα δύο και το πέρασμα από το ένα στο άλλο, δίνεται από τους μετασχηματισμούς του Lorentz.
Ας δούμε τώρα με ποιο τρόπο περιγράφουν ό,τι συμβαίνει μέσα στον ανελκυστήρα οι δυο παρατηρητές: Ο εσωτερικός και ο εξωτερικός.
Ο εξωτερικός παρατηρητής σημειώνει την κίνηση του ανελκυστήρα καθώς και όλων των σωμάτων στα εσωτερικό του και τη βρίσκει σύμφωνη με τι νόμο της βαρύτητας του Νεύτωνα. Γι' αυτόν ή κίνηση δεν είναι ομαλή, αλλά επιταχυνόμενη, εξ αιτίας της δράσης του πεδίου βαρύτητας της γης.
Ωστόσο, κάποιος μέσα στον ανελκυστήρα, θα μπορούσε κάλλιστα να υποθέσει πως ο ανελκυστήρας του ηρεμεί και πως το σύστημα συντεταγμένων του είναι αδρανειακό.
Είναι αδύνατο να ρυθμίσουμε τη διαφορά των δυο παρατηρητών. Καθένας τους θα μπορούσε να διεκδικήσει το δικαίωμα να αναφέρει όλα τα γεγονότα στο Σ.Σ. του. Κι οι δυο περιγραφές θα μπορούσαν να έχουν την ίδια εσωτερική συνοχή.
Άρα λοιπόν είναι δυνατή μια συνεπής περιγραφή φυσικών φαινομένων σε δυο διαφορετικά Σ.Σ., ακόμα κι αν δεν κινούνται ομαλά το ένα ως προς το άλλο. Αλλά για μια τέτοια περιγραφή, πρέπει να λάβουμε υπ' όψη μας τη βαρύτητα, χτίζοντας κατά κάποιο τρόπο τη «γέφυρα» πού κάνει δυνατό το πέρασμα από το ένα Σ.Σ. στο άλλο. Το πεδίο βαρύτητας υπάρχει για τον εξωτερικό παρατηρητή· δεν υπάρχει όμως για τον εσωτερικό. Για τον εξωτερικό παρατηρητή υπάρχει η επιταχυνόμενη κίνηση του ανελκυστήρα μέσα στο πεδίο βαρύτητας, ενώ για τον εσωτερικό παρατηρητή υπάρχει ηρεμία και το πεδίο βαρύτητας είναι ανύπαρκτο. Αλλά η «γέφυρα», δηλαδή το πεδίο βαρύτητας πού κάνει δυνατή την περιγραφή στα δυο Σ.Σ., στηρίζεται πάνω στην ισοδυναμία της βαρείας και της αδρανούς μάζας. Χωρίς αυτήν, η σειρά των συλλογισμών που θέσαμε θα αποτύγχανε.
Ας φανταστούμε τώρα ένα αδρανειακό Σ.Σ., όπου ισχύει η αρχή της αδράνειας. Περιγράψαμε τι συμβαίνει σ' ένα ανελκυστήρα που βρίσκεται σ' ένα τέτοιο Σ.Σ. Τώρα αλλάζουμε την εικόνα μας. Κάποιος απ' έξω έδεσε ένα σχοινί στη στέγη του ανελκυστήρα και τραβάει με μια σταθερή δύναμη, προς την κατεύθυνση πού δείχνει το επόμενο σχήμα.
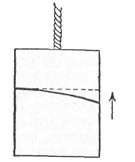
Εφ’ όσον οι νόμοι της μηχανικής ισχύουν σ' αυτό το Σ.Σ., ο ανελκυστήρας κινείται με σταθερή επιτάχυνση προς την κατεύθυνση της κίνησης. Ας ακούσουμε πάλι την εξήγηση πού δίνουν στα φαινόμενα που διαδραματίζονται μέσα στον ανελκυστήρα, ο εσωτερικός και ο εξωτερικός παρατηρητής.
Ο εξωτερικός παρατηρητής. Το Σ.Σ. μου είναι σύστημα αδράνειας. Ο ανελκυστήρας κινείται με σταθερή επιτάχυνση, εξ αιτίας της σταθερής δύναμης που δρα πάνω του. Ο εσωτερικός παρατηρητής βρίσκεται σε απόλυτη κίνηση. Γι' αυτόν δεν ισχύουν οι νόμοι της μηχανικής. Δεν βρίσκει ότι σώματα που δεν υφίστανται την επίδραση καμιάς δύναμης ηρεμούν. Αν αφήσει ένα σώμα να πέσει, χτυπάει αμέσως το πάτωμα του ανελκυστήρα, γιατί το πάτωμα επιταχύνεται προς το σώμα.
Ο εσωτερικός παρατηρητής. Ο ανελκυστήρας μου δεν βρίσκεται σε απόλυτη κίνηση. Παραδέχομαι πώς το Σ.Σ. μου, που είναι σταθερά δεμένο με τον ανελκυστήρα, δεν είναι πραγματικά σύστημα αδράνειας, αλλά αυτό δεν έχει σχέση με την απόλυτη κίνηση. Τα σώματα πέφτουν, γιατί ο ανελκυστήρας μου βρίσκεται μέσα σε ένα πεδίο βαρύτητας. Παρατηρώ ακριβώς τα ίδια είδη κινήσεων με έναν άνθρωπο πάνω στη γη.
Αυτές οι δυο περιγραφές έχουν λογική συνοχή και δεν υπάρχει δυνατότητα να αποφασίσει κανείς, ποια είναι αληθινή.
Υπάρχει άραγε τρόπος να βγει κανείς από το διφορούμενο των δυο περιγραφών και να αποφασίσει υπέρ της μιας απορρίπτοντας την άλλη; Ας υποθέσουμε πως μια φωτεινή ακτίνα εισέρχεται οριζόντια από ένα παράθυρο στον ανελκυστήρα και χτυπά στην απέναντι πλευρά, υστέρα από ένα συντομότατο χρονικό διάστημα. Ας δούμε τώρα πώς θα μπορούσε να προβλεφθεί από τους δυο παρατηρητές η τροχιά της φωτεινής ακτίνας.
Ο εξωτερικός παρατηρητής, πιστεύει πως ο ανελκυστήρας επιταχύνεται θα σκεφτόταν ως εξής: Η φωτεινή ακτίνα μπαίνει οριζόντια από το παράθυρο και κινείται ευθύγραμμα, με σταθερή ταχύτητα, προς την απέναντι πλευρά. Αλλά ο ανελκυστήρας κινείται προς τα πάνω και αλλάζει θέση την ώρα που η ακτίνα κινείται προς την πλευρά του. Η ακτίνα λοιπόν θα χτυπήσει ένα σημείο που δεν είναι ακριβώς απέναντι από το σημείο της εισόδου, αλλά λίγο πιο κάτω. Η διαφορά θα είναι ελάχιστη, ωστόσο θα υπάρχει, και η φωτεινή ακτίνα προχωρεί ως προς τον ανελκυστήρα όχι ευθύγραμμα, αλλά σε ελαφριά καμπύλη τροχιά. Η διαφορά οφείλεται στην απόσταση που διατρέχει ο ανελκυστήρας, ώσπου η ακτίνα να διανύσει το εσωτερικό του.
Ο εσωτερικός παρατηρητής, πιστεύει στην ύπαρξη πεδίου βαρύτητας που δρα σ' όλα τα αντικείμενα. Θα έλεγε πως δεν υπάρχει επιταχυνόμενη κίνηση του ανελκυστήρα. Υπάρχει μονάχα η δράση του πεδίου βαρύτητας. Αν θεωρούσε ότι μια φωτεινή ακτίνα δεν έχει βάρος και ότι δε θα επηρεαστεί από το πεδίο βαρύτητας, θα συμπέρανε ότι αν αυτή εισέλθει οριζόντια, θα χτυπήσει την πλευρά σε ένα σημείο, ακριβώς απέναντι από το σημείο εισόδου.
Από αυτά θα φαινόταν πως υπάρχει δυνατότητα να αποφασίσουμε ανάμεσα σ' αυτές τις δυο απόψεις, μια και το φαινόμενο θα μπορούσε να είναι διαφορετικό για τους δυο παρατηρητές. Αλλά υπάρχει ένα σοβαρό λάθος στη σκέψη του εσωτερικού παρατηρητή που σώζει το προηγούμενο συμπέρασμα: Μια φωτεινή ακτίνα μεταφέρει ενέργεια. Η ενέργεια έχει μάζα και κάθε αδρανής μάζα έλκεται από το πεδίο βαρύτητας, μια και η αδρανής και η βαρεία μάζα είναι ισοδύναμες. Μια φωτεινή ακτίνα θα καμπυλωθεί μέσα σ' ένα πεδίο βαρύτητας, ακριβώς όπως ένα σώμα που θα εκτοξευόταν οριζόντια με την ταχύτητα του φωτός.
Από τα παραδείγματα αυτά συνάγεται ότι είναι βάσιμη η ελπίδα να διατυπώσουμε μια σχετικιστική φυσική. Αλλά για να το κάνουμε, πρέπει πρώτα να πραγματευτούμε το πρόβλημα της βαρύτητας.
Η απόλυτη κίνηση και τα συστήματα αδράνειας μπορούν να εξαλειφθούν από τη φυσική, και μπορεί να διαμορφωθεί μια νέα σχετικιστική φυσική. Τα ιδεατά πειράματα που αναπτύξαμε φανερώνουν με ποιο τρόπο συνδέονται στενά το πρόβλημα της γενικής θεωρίας της σχετικότητας και το πρόβλημα της βαρύτητας, και γιατί η ισοδυναμία της βαρείας και της αδρανούς μάζας είναι τόσο ουσιαστική γι' αυτή τη σύνδεση. Οι νόμοι της βαρύτητας, όπως όλοι οι νόμοι της φύσης, πρέπει να διατυπωθούν για όλα τα δυνατά Σ.Σ., ενώ οι νόμοι της κλασικής μηχανικής, όπως διατυπώθηκαν από τον Νεύτωνα, ισχύουν μόνο στα συστήματα αδράνειας.
Μετάβαση σε άλλη ενότητα του άρθρου: