Επιστήμη - Επιστημολογία
- Το θεώρημα της μη πληρότητας και φιλοσοφικές προεκτάσεις
- Η ελευθερία του απροσδιόριστου
- Σχετικότητα και προεκτάσεις
- Θεωρία της σχετικότητας: οι έννοιες
- Κβαντομηχανική: έννοιες και ερμηνευτικά ρεύματα
- Eρμηνείες της κβαντoμηχανικής: Ο Schrodinger και η γάτα του
- Προς μια θεωρία των πάντων
- Οικοσύνθεση στον Άρη
- Διαλεκτική βιολογία
- Οι αντιλήψεις του Schrodinger για το "Τι είναι η ζωή"
Κβαντομηχανική: έννοιες και ερμηνευτικά ρεύματα
2) Η κυματοσυνάρτηση και η εξίσωση Schrödinger
Τα μαθηματικά για την περιγραφή των κβαντικών φαινομένων μπορούν να διατυπωθούν με πολλούς τρόπους, αλλά ο πιο κλασικός είναι αυτός που στηρίζεται στην εξίσωσή του και στην κυματοσυνάρτηση ψ.
Η ακτινοβολία του μέλανος σώματος και το φωτοηλεκτρικό φαινόμενο οδήγησαν τον Bohr στην διατύπωση της αρχής της κβάντωσης της ενέργειας στον μικρόκοσμο. Ως κβαντωμένα μεγέθη ήδη ήταν γνωστές οι συχνότητες συντονισμού χορδών, όπως π.χ. των χορδών μιας κιθάρας με σταθερά άκρα, τα λεγόμενα στάσιμα κύματα, οπότε ο de Broglie διατύπωσε την άποψη της κυματικής φύσης της ύλης, και αυτός με την σειρά του οδήγησε τον Schrodinger στην διατύπωση της κυματικής εξίσωσης, πού περιγράφει την εξέλιξη ενός κβαντικού συστήματος.
Η εξίσωση του Schrodinger έχει την μορφή
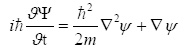 |
(1) |
|---|
Η εξίσωση αυτή περιγράφει την εξάρτηση από την θέση και τηνεξέλιξη στον χρόνο της συνάρτησης ενός συστήματος και συμβολίζεται ως ψ(x,y,z,t). H συνάρτηση που αντιστοιχεί σε ένα κβαντικό σύστημα ονομάζεται κυματοσυνάρτηση, επειδή είναι ανάλογη με τις συναρτήσεις που περιγράφουν την εξέλιξη των κυμάτων στην κλασική φυσική. Σε κάθε φυσικό σύστημα, μπορούμε να παρατηρήσουμε κάποια χαρακτηριστικά του φυσικά μεγέθη, π.χ. ταχύτητα, θέση, ορμή. H ψ υπολογίζεται από την εξίσωση του Schrodinger και μας δίνει την δυνατότητα να τα υπολογίσουμε.
Υπάρχει μία ψ για κάθε κατάσταση του κβαντικού μας συστήματος και αντίστροφα για κάθε ψ αντιστοιχεί μία κατάσταση του συστήματος. Γνωρίζοντας την ψ ενός συστήματος μπορούμε να υπολογίσουμε όλα τα χαρακτηριστικά μεγέθη του συστήματος και τον τρόπο με τον όποιο αυτά εξελίσσονται στον χρόνο. Η ψ περιλαμβάνει όλη την πληροφορία την οποία μπορούμε να ανακτήσουμε από το σύστημα μας.
Στην κλασική φυσική η αντίστοιχη εξίσωση με αυτήν του Schrodinger είναι η εξίσωση κίνησης του Νεύτωνα. Από αυτήν παίρνουμε αριθμητικές τιμές για την θέση και την ταχύτητα ενός σώματος, μέσα στην εξέλιξη του χρόνου, όταν αυτό κινείται πάνω σε συγκεκριμένες τροχιές. Δεν συμβαίνει όμως το ίδιο σε ένα κβαντικό σύστημα, το οποίο περιγράφει η εξίσωση του Schrödinger, γιατί η τελευταία είναι μιγαδική: Στο αριστερό της μέρος υπάρχει το i (οπού i2=-1). Οι μιγαδικές λύσεις δεν μπορούν να αντιστοιχούν σε φυσικά μεγέθη του κλασικού κόσμου. Στον κβαντικό κόσμο, λοιπόν, δεν μας φανερώνουν παράδοξα γεγονότα μόνο τα πειράματα, άλλα και ο μαθηματικός φορμαλισμός θέτει ερμηνευτικά προβλήματα. Γιατί το ερώτημα τι είδους οντότητα είναι ένα σωματίδιο μεταξύ της αρχής και του τέλους της διαδρομής, στην λεγόμενη κβαντική κατάσταση, είναι ισοδύναμο με το τι περιγράφει η κυματοσυνάρτηση, ποιο είναι το υποκείμενο της ψ.
Αν υποθέσουμε ότι έχουμε ένα τέτοιο κβαντικό σύστημα, π.χ. ένα ηλεκτρόνιο, το οποίο είναι απομονωμένο από το περιβάλλον του. Το σύστημα αυτό θα χαρακτηρίζεται από μια σειρά φυσικών μεγεθών, π.χ. ενέργεια, ταχύτητα, στροφορμή κ.τ.λ. Τα μεγέθη αυτά χαρακτηρίζουν την (αρχική) του κατάσταση. Όταν σε μια χρονική στιγμή ξέρουμε κάποια από αυτά τα μεγέθη, τότε με την βοήθεια της αντίστοιχης ψ μπορούμε να τα υπολογίσουμε σε μια επόμενη χρονική στιγμή και επομένως να γνωρίζουμε την κατάσταση του συστήματος μας. Για κάθε ένα από αυτά τα φυσικά μεγέθη υπάρχει ένας τελεστής, ο οποίος όταν εφαρμοσθεί στην ψ μάς δίδει έναν κανόνα αντιστοίχισης για το συγκεκριμένο φυσικό μέγεθος.
Σε σχέση με ένα φυσικό μέγεθος a (στο οποίο αντιστοιχεί ένας τελεστής Α), η ψ μπορεί να αναλυθεί σε ένα άθροισμα συναρτήσεων ψi που λέγονται ιδιοσυναρτήσεις του Α, και έχουν την ιδιότητα, η δράση του Α επί της ψi να έχει ως αποτέλεσμα απλά τον πολλαπλασιασμό της ψiεπί ένα πραγματικό αριθμό αi
| (2) |
|---|
| i=1,2, ... (3) |
|---|
Η ψi είναι μια από τις ιδιοσυναρτήσεις του τελεστή Α, που αντιστοιχούν στο φυσικό μέγεθος α. Ο αριθμός αiκαλείται ιδιοτιμή του τελεστή και είναι πραγματικός αριθμός, επειδή, αξιωματικά, οι τελεστές που περιγράφουν τα φυσικά μεγέθη είναι ερμιτιανοί τελεστές. Η φυσική σημασία των αi είναι οι διάφορες τιμές που μπορεί να πάρει το φυσικό μέγεθος α του συστήματος μας όταν προσπαθήσουμε να το μετρήσουμε. Η γνώση λοιπόν του ψ μας δίνει την δυνατότητα να γνωρίσουμε όλες τις δυνατές τιμές ενός φυσικού κβαντικού μεγέθους. Οι τιμές αυτές μπορεί να είναι άπειρες ή πεπερασμένες.
Η ψ είναι μια μιγαδική συνάρτηση και ως τέτοια, δεν έχει φυσικό νόημα. Το γινόμενο της όμως επί την συζυγή της, δηλαδή το τετράγωνο του μέτρου της, είναι πάντα πραγματικός αριθμός, ο |ψ|2 . Αυτό οδήγησε τον Born στην πιθανοκρατική ερμηνεία της ψ. Σύμφωνα με αυτήν η |ψ|2 περιγράφει τις πιθανότητες που έχει να πάρει ένα μέγεθος μια συγκεκριμένη τιμή. Με άλλα λόγια η διαδικασία επίλυσης της εξίσωσης του Schrödinger δεν μας δίδει μόνο τις τιμές που μπορεί να πάρει ένα φυσικό μέγεθος ενός κβαντικού συστήματος, άλλα και το πόσο πιθανή είναι η κάθε τιμή.
Αν λοιπόν θελήσουμε να μετρήσουμε το φυσικό μέγεθος α, σε κάποια συγκεκριμένη χρονική στιγμή και σε συγκεκριμένη θέση, τότε στο μετρητικό μας όργανο θα πάρουμε, μία από τις τιμές αi που μας δίδουν οι εξισώσεις (1), (2) και (3), τις ιδιοτιμές δηλαδή του Α. Σε κάθε φυσικό μέγεθος μπορεί να αντιστοιχούν πολλές ιδιοσυναρτήσεις και επομένως ιδιοτιμές. Υπάρχουν μεγέθη, όπως η ιδιοστροφορμή (σπιν), που μπορεί να πάρει πεπερασμένο αριθμό τιμών, και επομένως ο τελεστής της ιδιοστροφορμής έχει πεπερασμένο αριθμό ιδιοσυναρτήσεων και ιδιοτιμών.
Όταν κάνουμε λοιπόν μια μέτρηση, η τιμή αi του φυσικού μεγέθους α έχει πιθανότητα |ψ(αi)|2 = |ci|2 να εμφανισθεί στα όργανα μέτρησης. Αν κάνουμε ένα αρκετά μεγάλο αριθμό μετρήσεων, θα δούμε ότι η κάθε τιμή του μεγέθους που μετρούμε θα είναι μία από αυτές που μας λένε οι εξισώσεις (1) και (2) και στο τέλος θα εμφανισθούν όλες και με την συχνότητα που μας δίνει οκανόνας του Born.
Έτσι η δράση ενός (ειδικού) τελεστή επί της ψ έχει ως αποτέλεσμα τον υπολογισμό όλων των δυνατών τιμών μιας μέτρησης καθώς και των πιθανοτήτων που αντιστοιχούν σε κάθε μια από αυτές (π.χ. της ταχύτητας, ή της ενέργειας, ή της θέσης ενός σωματιδίου), μετά από την παρέλευση ενός χρόνου t, εφόσον γνωρίζουμε την τιμή των αντίστοιχων μεγεθών στην αρχή του χρονικού διαστήματος. Η αφηρημένη αυτή μαθηματική περιγραφή, σε ειδικές περιπτώσεις μπορεί να υπολογισθεί αριθμητικά και να έχουμε συγκεκριμένα νούμερα. Αυτό όμως είναι σπάνιο. Στην πραγματικότητα αυτή η μαθηματική περιγραφή έχει μάλλον ποιοτικό χαρακτήρα.
Ας κάνουμε όλα τα παραπάνω πιο σαφή. Ας υποθέσουμε ότι ένα κβαντικό μέγεθος μπορεί να πάρει δύο τιμές, α και β με αντίστοιχες ιδιοσυναρτήσεις ψα και ψβ. Εάν ψ η κυματοσυνάρτηση του συστήματος τότε:
| (4) |
|---|
Επομένως τα |cα|2 και |cβ|2 μας δίνουν τις πιθανότητες που υπάρχουν ώστε κατά την μέτρηση μας να πάρει το μέγεθος αυτό μία από τις δύο αυτές τιμές, ας υποθέσουμε 30% για την α και 70% για τη β. Γράφουμε με βάση την (2),
| (5) |
|---|
Αυτό δεν σημαίνει ότι σε κάθε μέτρηση έχουμε 30% α και 70% β, αλλά α ή β. Απλά, αν κάνουμε πάρα πολλές μετρήσεις σε άπειρα στον αριθμό πανομοιότυπα συστήματα, στο 30% του συνόλου των μετρήσεων θα μετρήσουμε την τιμή α και στο 70% θα βρούμε την τιμή β.
Όταν π.χ. ένα ηλεκτρόνιο φθάνει στο τέρμα της διαδρομής του, λέμε ότι δρα ο τελεστής που αντιστοιχεί στην φωτοευαίσθητη πλάκα και παίρνουμε την συγκεκριμένη κατανομή των κροσσών συμβολής. Αν π.χ. κάνουμε ενδιάμεση μέτρηση για να δούμε από ποια σχισμή περνά το ηλεκτρόνιο, πάλι λέμε ότι δρα ένας άλλος τελεστής και η δράση του μας δίνει τα αποτελέσματα πού βλέπουμε.
Η συσχέτιση της |ψ|2 , με την κατανομή των πιθανοτήτων να πάρει ένα μέγεθος μια συγκεκριμένη τιμή, ήταν και η πρώτη προσπάθεια να απαντηθεί το ερώτημα της προηγούμενης παραγράφου. Δηλαδή θεωρήθηκε ότι η ψείναι ένα κύμα πιθανότητας. Έχουμε ένα κύμα πιθανότητας που, π.χ. στο πείραμα των δύο σχισμών, χωρίζεται στα δύο και περνώντας από τις σχισμές συμβάλλει με τον εαυτό του και παράγει τα φαινόμενα συμβολής. Μια τέτοια ερμηνεία όμως βασίζεται σιωπηρώς στο ότι οι πιθανότητες, π.χ., που έχει ένα σωματίδιο να βρεθεί σε μια συγκεκριμένη θέση στον χώρο, έχουν κάποιου είδους υπόσταση, σαν να είναι κάποιου είδους υλικό κύμα, πού πυκνώνει και αραιώνει και παράγει κυματισμούς. Κάτι τέτοιο, σαν γενική τάση, δεν γίνεται δεκτό και έτσι η πιθανοκρατική ερμηνεία γίνεται συνήθως δεκτή μόνο στο υπολογιστικό μέρος της, όπου λειτουργεί εντυπωσιακά.
Μία άλλη σημαντική κβαντική ιδιότητα είναι το ότι η εξίσωση του Schrodinger είναι γραμμική:
Αν ψ1, ψ2,... είναι λύσεις της εξίσωσης Schrodinger, τότε και ο γραμμικός συνδυασμός τους:
ψ = c1ψ1 + c2ψ2 + ... είναι επίσης λύση που ικανοποιεί τις ίδιες συνοριακές συνθήκες (υπέρθεση, επαλληλία).
Η φυσική σημασία της γραμμικότητας είναι πολύ σημαντική και μπορεί να νοηθεί με δύο τρόπους:
1) Ότι μια κβαντική οντότητα καθώς εξελίσσεται στον χρόνο αναλύεται σε αντίγραφα του εαυτού της και το καθένα ακολουθεί μία από τις διαδρομές που προβλέπει η ψ. Κάθε αντίγραφο εξελίσσεται εντελώς ανεξάρτητα από τα αλλά αντίγραφα. Αυτό εξηγεί πολλά από τα κβαντικά παράδοξα και είναι γνωστό στο ευρύ κοινό, ως το ότι ένα σωματίδιο μπορεί να είναι ταυτόχρονα σε περισσότερες της μιας θέσεις. Έτσι π.χ. λέμε ότι στο πείραμα των δύο σχισμών το σωματίδιο περνά κατά το ήμισυ από την μια σχισμή και κατά το ήμισυ από την άλλη.
2) Ότι μια σύνθετη οντότητα που αποτελείται από κβαντικές οντότητες θα είναι και αυτή κβαντική. Και αυτό έχει μεγάλη σημασία, όπως θα δούμε στην συνέχεια.
Μετάβαση σε άλλη ενότητα του άρθρου: