Θα πλησιάσουμε τώρα το ζήτημα της σύνδεσης ανάμεσα στη γενική θεωρία της σχετικότητας και τη γεωμετρία. Ας αρχίσουμε με την περιγραφή ενός επίπεδου δισδιάστατου κόσμου όπου ζουν μονάχα όντα δυο διαστάσεων τα οποία μπορούν να σκέφτονται και να παράγουν επιστήμη. Τα όντα αυτά είναι ανίκανα να φανταστούν έναν τρισδιάστατο χώρο, ακριβώς όπως εμείς είμαστε ανίκανοι να φανταστούμε ένα τετραδιάστατο. Μπορούμε να θλάσουμε και να καμπυλώσουμε γραμμές και επιφάνειες, δύσκολα όμως μπορούμε να φανταστούμε ένα τρισδιάστατο χώρο τεθλασμένο και καμπύλο.

Τα όντα αυτά θα μπορούσαν να αναπτύξουν τέλεια την ευκλείδεια επιπεδομετρία.

Ας φανταστούμε τώρα πώς τα δισδιάστατα αυτά όντα ζουν σε διαφορετικές συνθήκες. Ας φανταστούμε πώς κάποιος απ' έξω, από την «τρίτη διάσταση», τα μεταφέρει στην επιφάνεια μιας γιγάντιας σφαίρας. Αν τα οντά είναι πολύ μικρά σε σχέση με τη συνολική επιφάνεια, αν δεν έχουν κανένα μέσον τηλεπικοινωνίας κι αν δε μπορούν να πάνε πολύ μακριά, δε θα νιώσουν καμιά αλλαγή. Π.χ. σε δυο μικρούς, ομόκεντρους κύ­κλους, ο λόγος των περιφερειών είναι πάντα ίση με το λόγο των ακτινών. Ταξιδεύοντας σε ευθεία γραμμή, δεν θα ξαναρθούν ποτέ στο σημείο απ' όπου ξεκίνησαν.

Αλλά αν τα όντα αυτά αναπτύξουν στην πορεία του χρόνου τις θεωρητικές και τεχνικές γνώσεις τους και εφεύρουν μέσα επικοινωνίας που τους επιτρέπουν να διατρέχουν γρήγορα μεγάλες αποστάσεις, θα παρατηρήσουν τότε, πως πηγαίνοντας ίσια μπροστά, θα επιστρέφουν τελικά την αφετηρία τους. «Ίσια μπροστά» σημαίνει κατά μήκος ενός μέγιστου κύκλου της σφαίρας. Θα παρατηρήσουν επίσης πώς η σχέση των περιφε­ρειών δυο ομόκεντρων κύκλων δεν είναι ίση με τη σχέση των ακτινών τους, αν ο ένας από τους κύκλους είναι μικρός και ο άλλος μεγάλος.

Θα καταλάβουν τελικά πώς ο κόσμος τους είναι πεπερασμένος και πως κυβερνιέται από γεωμετρικές αρχές διαφορετικές από εκείνες που μάθανε. Ότι κόσμος τους είναι μια σφαιρική επιφάνεια με δυο διαστάσεις. Θα βαλθούνε να μάθουν νέες αρχές γεωμετρίας για τον δισδιάστατο χώρο τους, που αν και θα διαφέρουν τελείως από του Ευκλείδη, θα μπορούν να δια­τυπωθούν με την ίδια εσωτερική ενότητα και λογική.

Ας ξαναρθούμε τώρα στα τρισδιάστατα όντα του κόσμου μας. Ας φανταστούμε πως παρατηρήθηκαν ασυμφωνίες με την ευκλείδεια γεωμετρία, πως το άθροισμα π.χ. των γωνιών ενός μεγάλου τριγώνου, κατασκευασμένου με σταθερές ράβδους δεν είναι ίσο με δυο ορθές γωνίες. Θα έπρεπε να εγκαταλείψουμε την ιδέα πως ο χώρος μας είναι ευκλείδειος και να ζητήσουμε μία πιο πειστική εικόνα της πραγματικότητας.

Η ανάγκη αυτή μπορεί να φανεί με ένα ιδεατό πείραμα, που δείχνει πώς μια πραγματικά ρελατιβιστική φυσική, δεν μπορεί να θεμελιωθεί στην ευκλείδεια γεωμετρία.

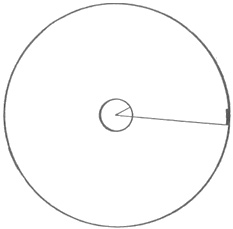
Ας φανταστούμε ένα μεγάλο δίσκο που πάνω του είναι χαραγμένοι δυο ομόκεντροι κύκλοι, ο ένας πολύ μικρός κι ο άλλος πολύ μεγάλος, και που το κοινό κέντρο τους συμπίπτει με το κέντρο του δίσκου. Ο δίσκος στρέφεται γρήγορα σχετικά με έναν εξωτερικά παρατηρητή (ο άξονας γύρω από τον όποιο στρέφεται ο δίσκος περνάει από το κέντρο του). Πάνω του στέκεται ένας εσωτερικός παρατηρητής. Υποθέτουμε ακόμα πως το Σ.Σ. του εξωτερικού παρατηρητή είναι σύστημα αδράνειας. Ο εξωτερικός παρατηρητής μπορεί να χαράξει στο Σ.Σ. του δυο κύκλους ίδιου μεγέθους με τους κύκλους του στρεφόμενου δίσκου.

Η ευκλείδεια γεωμετρία ισχύει στο Σ.Σ. του, μια και είναι σύστημα αδράνειας. Έτσι θα βρει πως ο λόγος των περιφερειών είναι ίσος με το λόγο των ακτινών. Τι γίνεται όμως με τον παρατηρητή πάνω στα δίσκο; Από την άποψη της κλασικής φυσικής, αλλά και της ειδικής θεωρίας της σχετικότητας, το Σ.Σ. του είναι απαγορευμένο. Αλλά αν έχουμε την πρόθεση να βρούμε νέους τύπους για τους νόμους της φυσικής που να ισχύουν σε οποιοδήποτε Σ.Σ., οφείλουμε να πάρουμε το ίδιο στα σοβαρά, τόσο τον παρατηρητή πάνω στα δίσκο, όσο και τον εξωτερικό παρατηρητή. Απ' έξω, κοιτάμε τον εσωτερικό παρατηρητή, που προσπαθεί να μετρήσει το μήκος των περιφερειών και των ακτινών πάνω στον περιστρεφόμενο δίσκο. Χρησιμοποιεί τον ίδιο κανόνα με τον εξωτερικό παρατηρητή. «Τον ίδιο» σημαίνει, ή πραγματικά τον ίδιο κανόνα που ο εξωτερικός παρατηρητής δίνει στον παρατηρητή του δίσκου, ή τον ένα από δυο κανόνες που έχουν το ίδιο μήκος όταν βρίσκονται σε ηρεμία σε ένα Σ.Σ.

Ο εσωτερικός παρατηρητής πάνω στο δίσκο αρχίζει να μετράει την ακτίνα και την περιφέρεια του μικρού κύκλου. Τα μέρη του δίσκου κοντά στο κέντρο έχουν πολύ μικρές ταχύτητες. Αν ο κύκλος είναι πολύ μικρός, ο κανόνας έχει το ίδιο μήκος για τον εξωτερικό και για τον εσωτερικό παρατηρητή και το αποτέλεσμα των μετρήσεων τους θα 'ναι το ίδιο και για τους δυο. Ο παρατηρητής πάνω στο δίσκο, μετράει τώρα την ακτίνα του μεγάλου κύκλου. Ο κανόνας τοποθετημένος πάνω στην ακτίνα, βρίσκεται σε κίνηση ως προς τον εξωτερικό παρατηρητή. Ένας τέτοιος κανόνας δεν θα υποστεί συστολή γιατί η διεύθυνση της κίνησης είναι κάθετη προς τον κανόνα. Τρεις μετρήσεις λοιπόν, δηλαδή των δυο ακτινών και της μικρής περιφέ­ρειας, είναι ίδιες και για τους δυο παρατηρητές. Αλλά δεν συμβαίνει το ίδιο και με την τέταρτη μέτρηση. Το μήκος της μεγάλης περιφέρειας θα είναι διαφορετικό για τους δυο παρατηρητές. Ο κανόνας πού είναι τοποθετημένος πάνω στην περιφέρεια, κατά την κατεύθυνση της κίνησης, θα φαίνεται πιο κοντός για τον εξωτερικό παρατηρητή, αν τον συγκρίνει με τον ακίνητο κανόνα του. Η τα­χύτητα του μεγάλου κύκλου είναι πολύ πιο μεγάλη από του μικρού και η συστολή πρέπει να ληφθεί υπ' όψη. Αν λοιπόν εφαρμόσουμε τα αποτελέσματα της ειδικής θεωρίας της σχετικότητας, το συμπέρασμα μας θα είναι ότι το μήκος της μεγάλης περιφέρειας, μετρούμενο από τους δυο παρατηρητές, πρέπει να είναι διαφορετικό. Έτσι ο λόγος των δυο ακτίνων δεν είναι ίσος με τον λόγο των δυο περιφερειών για τον παρατηρητή του δίσκου, όπως είναι για τον εξωτερικό παρατηρητή! Ο παρατηρητής πάνω στο δίσκο, δεν μπορεί να επιβεβαιώσει την ισχύ της ευκλείδειας γεωμετρίας στο Σ.Σ. του.

Αφού έφτασε σ' αυτό το συμπέρασμα ό παρατηρητής πάνω στο δίσκο, θα μπορούσε να πει πως δεν επιθυμεί να έχει ένα Σ.Σ. οπού δεν ισχύει η ευκλείδεια γεωμετρία. Η κατάρρευση της ευκλεί­δειας γεωμετρίας οφείλεται στην απόλυτη περιστροφή, στο γεγονός πώς το Σ.Σ. του είναι απαγορευμένο. Όταν όμως σκέφ­τεται μ' αυτό τον τρόπο, ό παρατηρητής απορρίπτει τη βασική ιδέα της γενικής θεωρίας της σχετικότητας. Αν όμως θέλουμε να απορρίψουμε την απόλυτη κίνηση και να διατηρή­σουμε την ιδέα της γενικής θεωρίας της σχετικότητας, πρέπει να οικοδομήσουμε τη φυσική πάνω στη βάση μιας γεωμετρίας γενικότερης από του Ευκλείδη. Δεν υπάρχει τρόπος να ξεφύγουμε απ' αυτή τη συνέπεια, αν όλα τα Σ.Σ. είναι επιτρεπτά.

Οι μεταβολές που επέφερε η γενική θεωρία της σχετικότητας, δεν περιορίζονται μονάχα στο χώρο. Στην ειδική θεωρία της σχετικότητας είχαμε ρολόγια που ηρεμούσαν σε κάθε Σ.Σ., που είχαν τον ίδιο ρυθμό, και που ήταν συγχρονισμένα - έδειχναν δηλαδή την ίδια ώρα. Τι γίνεται με ένα ρολόι σ' ένα Σ.Σ. πού δεν είναι σύστημα αδράνειας; Θα χρησιμοποιήσουμε πάλι το ιδεατό πείραμα με τον περιστρεφόμενο δίσκο. Ο εξωτερικός παρατηρητής έχει στο σύστημα αδράνειας του τέλεια ρολόγια, που προχωρούν όλα με τον ίδιο ρυθμό και είναι συγχρονισμένα. Ο παρατηρητής πάνω στο δίσκο παίρνει δυο όμοια ρολόγια και τα τοποθετεί, το ένα πάνω στη μικρή περιφέρεια, και τ' άλλο πάνω στη μεγάλη. Το ρολόι πάνω στη μικρή περιφέρεια έχει πολύ μικρή ταχύτητα σε σχέση με τον εξωτερικά παρατηρητή. Μπορούμε λοιπόν να συμπεράνουμε πως ο ρυθμός του θα είναι ίδιος με του εξωτερικού ρολογιού. Αλλά το ρολόι που είναι τοποθετημένο πάνω στη με­γάλη περιφέρεια, έχει μια σημαντική ταχύτητα κι αυτό κάνει να αλλάζει ο ρυθμός του ως προς τα ρολόγια του εξωτερικού παρατη­ρητή και κατά συνέπεια και ως προς το ρολόι που είναι πάνω στη μικρή περιφέρεια. Τα δυο περιστρεφόμενα ρολόγια θα 'χουν λοιπόν διαφορετικό ρυθμό. Εφαρμόζοντας τα αποτελέσματα της ειδικής θεωρίας της σχετικότητας, βλέπουμε πάλι πως στο περιστρεφόμενο Σ.Σ. δεν μπορούμε να κάνουμε διευθετήσεις όμοιες μ' αυτές πού γίνονται σ' ένα σύστημα αδράνειας.

Ας δούμε και μια άλλη παράμετρο του προβλήματος: Ο εσωτερικός παρατηρητής νιώθει μια δύναμη να τον τραβάει από το κέντρο προς την περιφέρεια. Αλλά θεωρεί υπεύθυνο γι' αυτό ένα παράξενο πεδίο βαρύ­τητας που κατευθύνεται προς το εξωτερικό του δίσκου, παραμορφώνει τις σταθερές ράβδους και μεταβάλλει τα ρυθμό των ρολογιών του. Για αυτόν, το πεδίο βαρύτητας, η μη ευκλείδεια γεωμετρία και τα ρολόγια με διαφορετικούς ρυθμούς συνδέονται στενά μεταξύ τους. Όταν δεχόμαστε ένα οποιοδήποτε Σ.Σ., οφείλουμε ταυτόχρονα να δεχόμαστε και την ύπαρξη ενός κατάλληλου πεδίου βαρύτητας, και την επίδραση του στις σταθερές ράβδους και τα ρολόγια.

Στη γενική θεωρία της σχετικότητας δεν μπορούμε να χρησιμοποιήσουμε δομή με τους παράλληλους και κάθετους κανόνες και τα συγχρονισμένα ρολόγια, όπως στην ειδική θεωρία της σχετικότητας. Σε ένα αυθαίρετο Σ.Σ. δεν μπορούμε να καθορίσουμε το σημείο και τη χρονική στιγμή ενός γεγονότος, με τη βοήθεια σταθερών κανόνων και ρυθμικών, συγχρονισμένων ρολογιών, όπως στο σύστημα αδράνειας της ειδικής θεωρίας της σχετικότητας. Μπορούμε πάντα να διευθετούμε τα γεγονότα με τη βοήθεια των μη ευκλείδειων κανόνων μας και των ρολογιών που ο ρυθμός τους αλλάζει. Αλλά πραγματικές μετρήσεις, που απαιτούν σταθερούς κανόνες και τέλεια ρυθμικά και συγχρονισμένα ρολόγια, δεν μπορούν να πραγματοποιηθούν παρά σε τοπικά συστήματα αδράνειας. Γι' αυτό ισχύει ολόκληρη η ειδική θεωρία της σχετικότητας, αλλά το «καλό» μας Σ.Σ. είναι μόνο τοπικό, γιατί ο χαρακτήρας του σαν συστήματος αδράνειας, είναι περιορισμένος τοπικά και χρονικά. Ακόμα και στο αυθαίρετο Σ.Σ. μας, μπορούμε να προβλέψουμε τα αποτελέσματα των μετρήσεων πού πραγματοποιούνται στο τοπικό σύστημα αδράνειας. Αλλά για να γίνει αυτό, πρέπει να ξέρουμε το γεωμετρικό χαρακτήρα του χωροχρονικού συνεχούς.  

Τα ιδεατά μας πειράματα αποκαλύπτουν το γενικό χαρακτήρα της νέας σχετικιστικής φυσικής. Μας δείχνουν ότι το θεμελιώδες πρόβλημα είναι το πρόβλημα της βαρύτητας. Δείχνουν ακόμα πως η γενική θεωρία της σχετικότητας οδηγεί σε μια γενίκευση των εννοιών του χώρου και του χρόνου.

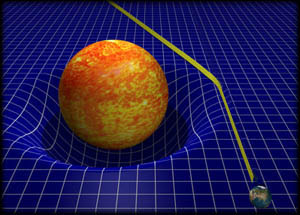
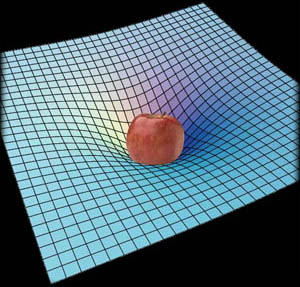
Συμπερασματικά, λοιπόν, ο χωροχρόνος έχει την ιδιότητα να καμπυλώνεται παρουσία ύλης όπως καμπυλώνεται ένα τεντωμένο σεντόνι όταν τοποθετήσουμε πάνω του μια μπάλα. Αν εκτοξεύσουμε τώρα μια μικρή μπίλια πάνω στην επιφάνεια του σεντονιού τότε η τροχιά που θα διαγράψει η μπίλια προφανώς δεν θα είναι ευθύγραμμη αλλά καμπύλη. Η καμπύλωση της τροχιάς δεν οφείλεται στη βαρυτική έλξη που ασκεί η μπάλα στην μικρή μπίλια αλλά στην παραμόρφωση που προκάλεσε η μπάλα στην επιφάνεια του σεντονιού. Με τον ίδιο τρόπο μια μεγάλη μάζα (π.χ. ένα αστέρι) καμπυλώνει το χωροχρόνο γύρω της στο Σύμπαν. Έτσι όλα τα ουράνια σώματα δεν αναγκάζονται να κινούνται σε καμπύλες τροχιές λόγω της δύναμης που λέγεται βαρύτητα, αλλά ακολουθούν τις καμπύλες γραμμές του παραμορφωμένου χωροχρόνου. Όπως πολύ ωραία το έθεσε ένας μεγάλος φυσικός: «Η ύλη λέει στο χώρο πώς να καμπυλωθεί και ο χώρος λέει στην ύλη πώς να κινηθεί».

Τέλος άρθρου.